

This method that relies on no assumptions other than the geometry of the Earth's orbit around the Sun. It has a parallax of 0.772".Astronomers derive distances to the nearest stars (closer than about 100 light-years) by a method called stellar parallax. How far are the stars?Īpart from the Sun, currently the closest star to us is a small red dwarf M5 class star, Proxima Centauri. If it is possible to measure an object's parallax, its distance can be directly and quickly calculated using expression 2.1 above. Why do astronomers use the parsec and not the light year? Well the parsec is directly determined from geometry and trigonometry and does not depend upon an arbitrary time scale. As light travels at 300,000 km per second in a vacuum, the total distance light travels in a year is approximately:ģ.0 × 10^8 × 60 × 60 × 24 × 365 ≈ 9.46 x 10^15 m or almost 10 million million km. Recall that a light year is simply the distance that light travels in one year. Many people think that astronomers measure distances in light years. This gives a baseline of two astronomical units and an angle of 2 p. If you study the diagram above you will see that the greatest baseline ground-based astronomers can obtain is by observing the star at times six months apart. This is called proper motion and must be accounted for when determining parallaxes. Also stars actually do appear to move across the sky relative to other stars in a definite direction over time. Corrections have to be made for atmospheric refraction and the effects of "seeing". The angle of parallax for even the closest stars is always < 1.0 arcsec so careful observation and precision is required. In reality it is not quite so simple for several reasons. This produces the simple but effective relationship:īy measuring the parallax angle for a star, astronomers can then directly determine its distance. One parsec is the distance to a point in space that subtends a parallax angle of one arc second. Astronomers have defined a standard unit of distance to be the parsec (pc). The closer a star is to us, the larger its angle of parallax will be. So how do we actually use parallax (strictly speaking we call this trigonometric parallax) to find the distance to stars? The Parsec Therefore the Moon has an angular diameter of 30 x 60 = 1800 arcsec. ∴ 1 arcsec = 1/(60圆0) = 1/3600th of a degree.īy way of comparison, the Moon subtends an angle of about ½° or 30 arcminutes. There are 60 arcsecs in 1 arcminute and 60 arc minutes in 1 degree of arc. This then means that the Earth - star and Sun - star distances are the same, that is d.Īs the parallax angle for even the nearest stars is very small we use the unit arcsecond (also written as arcsec, as or "). For triangles with one very small angle we can apply the small angle approximation:
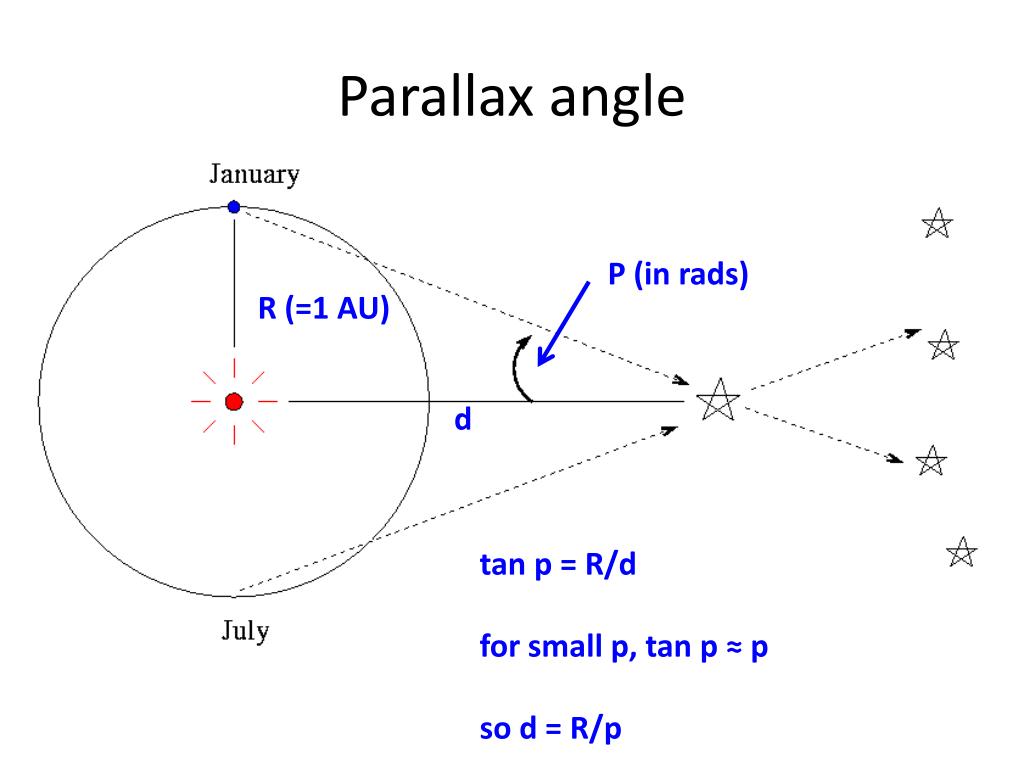
The parallax angle, p, is extremely small. In reality the triangle formed by the Earth at July, the Sun and the nearby star is much narrower as even the nearest star is at a large distance. The diagram above shows how a nearby star appears to shift relative to more distant background stars.ĬAREFUL: This diagram IS NOT TO SCALE. The diagram below shows the apparent shift of a nearby star to an observer on the Earth as it orbits the Sun. It can however, be measured directly by applying simple trigonometry. As you can see then, the distance to a star cannot be determined by its brightness (or size on photographic plate or CCD image). The reason that star B appears to move is that it is closer to us than the other stars, even though star A is brighter. The first measurement of parallax was not made until 1838. He correctly inferred that this was due to the vast distance to stars. Even Galileo was unable to detect any stellar motion when he used a telescope. The parallax of stars was predicted by Copernicus' heliocentric model but was not observed with the naked-eye. What happens to this parallax shift if you move your finger out to arms length? When you open that and close the right eye, the finger shifts to the right. As you close your left eye, the finger seems to shift to the left. You can try this yourself by holding a finger about 20 cm from your face and look at its position relative to a more distant object. This shift in a star's relative position is due to parallax.

If you said it is due to our orbit around the Sun you would be correct.

What could account for this shift in position? Parallax Imagine that this to and fro motion took place over 12 months. When you remove your mouse from the image it appears to move back to its original relative position. Place your mouse pointer over the image and observe what happens.Īs you can see, Star B appears to move relative to the other stars. Star A is brighter than B so must be closer. Star A is much larger than B so should be closer.Ģ.


 0 kommentar(er)
0 kommentar(er)
